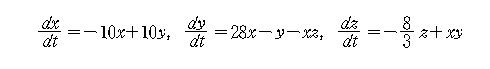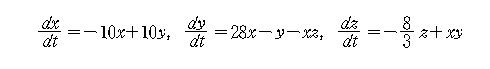Chaos simulator 개발에 관한 연구
A Study on a Development of Chaos Simulator
조 현상 (Cho, Hyun-Sang), 1996. 경원대학교 신문사 자연과학부분 논문대상
3.4. 갈래질 (Bifurcation)
3.4.1. Logistic / Trigonometric map
3.4.2. bifurcation diagram 각 부분에서의 attractor와 시계열 데이터의 상태.
IV. 카오스 시뮬레이터 CHS-96.
4.1. 개요.
4.2. Menu 구조.
V. 결 론.
참고 문헌.
I. 서 론.
사물의 운동을 미분방정식으로 기술하여 해석하고자 하는 뉴튼 패러다임의 시도는 산업혁명을 거쳐 현재에 이르기까지 현대 문명을 이루어 온 근간이었다.
그러나, 미분방정식의 성공적인 해석은 그 계(system)가 선형(linear)적일 경우에만 가능하다. 전자회로에서 가장 단순한 소자인 저항조차 실제로는 비선형적이며, 해석학은 계의 비선형적인 영역을 '제어 불능'영역으로 간주하고 비교적 선형에 가까운 영역만을 '선형근사화'하여 이용해 왔다.
그러나, 학문의 각 분야에서 이러한 결정론적인 계로서의 해석은 모순된 현실에 직면하게 되었다.
측정의 절대성은 아인시타인의 패러다임에 의해, 고착된 한계점은 양자물리학의 패러다임에 의해 붕괴되었으며, 근래에는 '결정론적인 계에서 유발되는 확률적인 현상'으로서 '혼돈(Chaos)이론'이 결정론적인 인과성에 대한 새로운 패러다임으로 등장했다.
혼돈현상은 결정론적인 계가 가지고 있는 비선형성에 기인하며 자연의 대부분의 실제 계는 비선형적이다. 이러한 비선형성은 이른바 혼돈현상으로 이름 지워지는 예측 불가능성, 일견 엉클어져 있으나 구조적으로 안정한 strange attractor등의 특성을 유발한다.
개별소자에서의 혼돈만이 아니라, 최근, 산타페 연구소(Santa Fe Institute)를 중심으로 연구되고 있는 복잡성의 과학(Science of complexity)은 혼돈현상을 포함하는 복잡한 계에 대한 새로운 형태의 학제간 연구과제로 발전되고 있다.
유체 역학이나 생물체의 신경계등을 포함하는 실세계의 동역학을 파악하기 위해서는 그들이 가지고 있는 비선형성에 대한 연구, 즉, 혼돈이론에 대한 연구는 더 이상 외면할 수 없는 주제가 되고 있다.
더군다나 혼돈현상은 수학이나 물리와 같은 특정한 학문영역에서만 나타나고 다루어질 주제가 아니며, 사회 과학과 공학을 망라하는 거의 모든 영역에서 발견되고 연구되어질 주제이다.
혼돈현상에 대한 초기의 연구가 벽에 부딪친 일반적인 원인이 그 해구조가 갖는 복잡성과 낯설음에 있다고 할 때, 혼돈현상에 대한 일반적인 이해와 그것을 바탕으로 하는 기초적인 연구에 대해 손쉽게 접근할 수 있는 컴퓨터 시뮬레이터(Computer Simulator)의 개발이 필요시 될 것이다.
본 연구는 이러한 필요성에 대해 혼돈현상의 일반적인 특징을 그래픽으로 구현하며, 외부의 데이터에 대해 동일한 분석을 행할 수 있는 기본적인 simulator의 개발과 그 과정을 통한 혼돈 현상의 기본적인 이해를 목적으로 하고 있다.
이와 같은 목적을 위해 본 고에서는 II장에서 혼돈현상 연구의 간단한 역사와 함께 III장에서 혼돈현상의 일반적인 특징을 서술하고 그 simulation 결과를 단계별로 도시할 것이며, 마지막으로 IV장에서 전체적인 simulator 항목의 계층 구조를 서술할 것이다.
II. 카오스 이론 연구의 역사.
혼돈현상은 1887년 스웨덴의 오스카 2세가 제시한 태양계의 안정성에 대한 프랑스 수학자 앙리 푸앙카레 (Henri Poincar'e )의 제한 삼체 운동에 대한 연구에서 기인한다고 할 수 있다.
무한대의 두 질량 중심에 대한 무한소 질량의 한 질점의 운동인 제한 삼체 운동은 적분불능이며 따라서 기존의 함수로는 해를 나타낼 수 없다.
푸앙카레는 이 역학계의 운동을 조사하기 위해 푸앙카레 단면 (Poincar'e section, 주기적 해가 한 주기마다 통과하는 위상공간상의 절단면)을 도입했는데 이때가 나타난 해의 경로가 바로 혼돈계의 특징, 즉 겹쳐지지 않는 무한개의 경로를 나타냈다.
이러한 복잡한 해의 경로를 해석하는 과정에 적용되어 발전하게 된 수학의 한 분야가 위상수학(Topology)이다.
그러나, 무한개의 해의 궤도를 추적한다는 것은 모든 계산을 수작업에 의존한 당시의 기술수준으로는 무리한 일이었다. 따라서, 푸앙카레의 이 발견은 이후 상당한 기간 동안 어둠 속에 묻혀있게 된다.
1960년대에 이르러 미국의 스메일(Stephen Smale)은 위상공간(Phase space, 계의 동역학적 경로를 나타내는 추상 공간)에서의 동역학계(dynamical system)의 운동형식에 대해 위상초상(phase portrait)을 통한 정성적인 기하학적 해석을 시도하던 중
기존의 세 가지 형태의 끌개(attractor, 충분히 과도 시간이 흐른 후 동역학계가 귀착되는 상태, 기존의 끌개란, 점끌개/순환끌개/준주기 끌개를 말함 → 3.2.) 이외에 새로운 형태의 끌개가 존재함을 알게 되었다.
이 새로운 형태의 끌개는 구조적인 안정성(structurally stable), 즉 견고함(robustness)과 이상함(strangeness)을 가지고 있으며, 타켄스(Floris Takens)와 뤼엘(David Ruelle)에 의해 이상한 끌개(strange attractor)로 명명되었다.
1963년, 미국의 대기과학지(Journal of the Atmospheric science) 3월호에 로렌츠(Edward Lorenz)의 '결정론적 비주기적 흐름(Deterministic Nonperiodic Flow)'이라는 논문이 게재되었다.
여기에서 로렌츠는 '나비효과(butterfly effect)'에 대해 언급한다. 로렌츠가 다루었던 방정식은 살츠만의 대류방정식에서 유도된 3원1차비선형연립미분방정식 (→3.1)이었으며 여기서 계의 동역학적 상태는 일정한 영역을 벗어나지 않으나 초기값에 민감한 특징을 보였다.
결국, 날씨를 나타내는 계가 아무리 간단한 방정식으로 나타내어진다 할지라도 비선형항을 포함하고 있는 이상 초기값의 정밀도에 따라 strange attractor의 특성에 기인한 나비효과에 의해 일정 시간 범위 이상의 장기 예보는 불가능한 것이 된다.
로렌츠의 연구 결과는 1975년 12월 American Mathematical Monthly에 발표된 요크(James Yorke)와 이천암의의 '주기 3은 혼돈을 의미한다. (Period Three implies 'Chaos'.)'라는 연구의 중요한 배경이 되는데, (→3.4.)
요크는 이 논문을 통해 혼돈현상을 최초로 'Chaos'로 명명한다.
이 논문의 주요 내용은 계의 시계열 데이터가 변수의 변화에 따라 3주기의 해를 가지는 상태가 있다면, 여기에는 Chaos 상태가 발생하고 있음을 말하고 있다.
본 고에서는 1976년 6월에 Nature지에 발표되어 큰 반향을 일으킨 수리생물학자 메이(Robot May)의 논리사상(Logistic map)과 삼각사상(Trigonometric map)을 통하여 이것을 확인할 것이다.
메이의 logistic map은 갈래질 분기도(Bifurcation diagram)의 대표적인 모델이 되어준다.
미국의 물리학자 파이겐바움(Mitchell Fiegenbaum)은 완전히 상이한 두 개의 혼돈계의 bifurcation diagram에서 동일한 축척률(Scaling, 주기 배증이 일어난 변수와 다음의 주기 배증이 일어나는 매개변수의 값까지의 비, Feigenbaum eigenvalue : 4.669201609)을 발견했다.
이것은 자기 상사구조(self-similarity)를 갖는 혼돈현상의 기저에 존재하는 규칙성에 대한 하나의 예를 보여준다.
Bifurcation diagram을 관찰하면 값들이 넓게 분포하는 혼돈영역의 중간 중간에 해의 값이 띠처럼 끊겨있는 부분(주기성 창문, periodic window)을 볼 수 있다.
주기성 창문을 확대 해 보면 그 내부에 전체 구조와 동일한 형태의 주기 배증이 일어나고 있음을 볼 수 있다.
strange attractor의 푸앙카레 단면의 경우와 마찬가지로 이 같은 자기상사구조를 만델블로트에 의해 명명된 쪽거리(fractal)라 한다.
칸토어 집합과 줄리아 집합을 포함하여 혼돈의 또다른 동전의 이면인 fractal 도형도 중요한 특성을 가지고 있다. 그러나, 본 고에서는 fractal에 대해서 별도로 다루지 않는다.
III. 카오스 현상의 일반 개요 / 해석.
3.1. Takens Embedded theorem.
타켄스 매립정리는 시간지연, 시간 적분방법이라고도 하며 자연계에서 쉽게 얻어지는 시계열 데이터를 각 차원의 수만큼 지연시켜 좌표계를 구성하므로써 쉽게 위상공간상의 attractor를 구성할 수 있게 해준다.
전술한 바와 같이, attractor에 관한 스메일의 연구 방향은 '미분방정식계'에 관한 '해석학적' 접근에 대해 '동역학계'에 관한 '기하학적'인 접근이라고 할 수 있다.
위상공간에서의 동역학해석의 중요성은 계의 특성을 파악하기가 용이하다는 것에 있다.
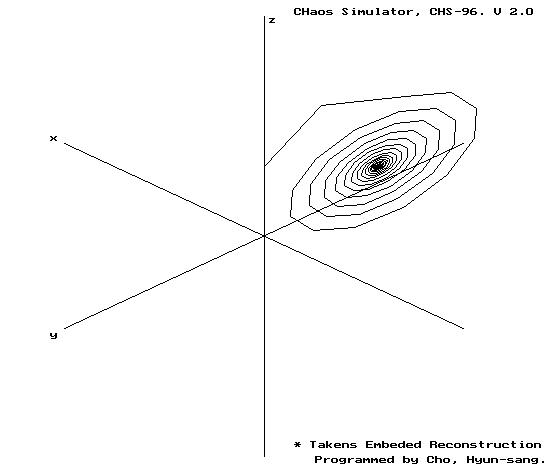
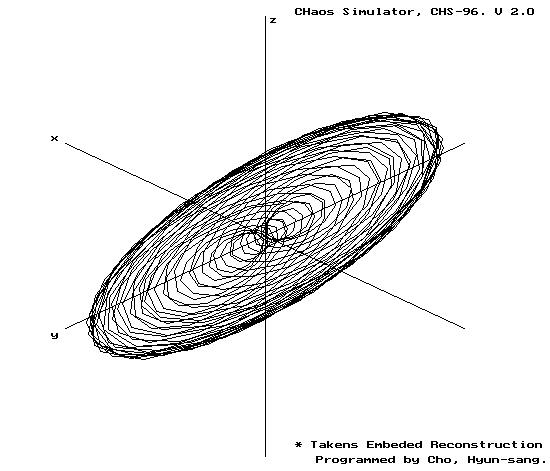
본 절에서는 Lorenz attractor의 3차원 실공간에서의 구성과 x축 변수의 값의 변화를 시간지연 재구성한 결과를 비교하므로써 타켄스 매립정리가 계의 위상적 특성을 보존하며 이 결과를 동역학계의 해석에 이용할 수 있음을 그림을 통해 보이기로 한다.
타켄스 매립정리의 수학적 정리는 다음과 같다.

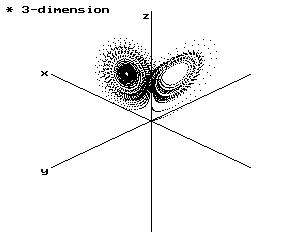
(a) 3차원 공간
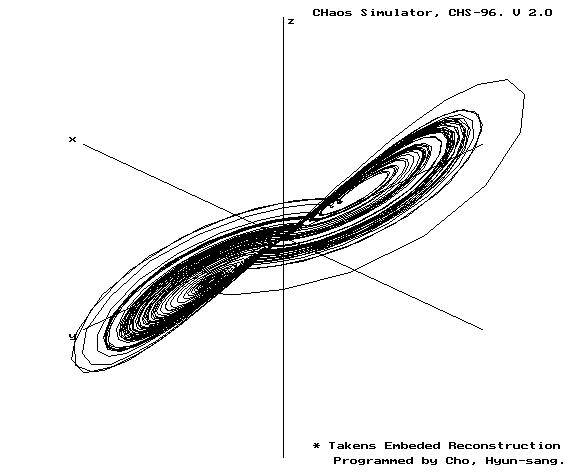
(b) 시간지연에 의한 재구성 (y-variable)
Fig. 1. 3차원 공간과 재구성된 Lorenz attractor의 구조
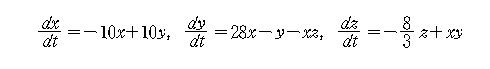
3.2. Attractor / Poincare 단면 분석.
II 장에서 언급한 바와 같이 동역학계에는 4가지 형태의 끌개(attractor)가 존재한다. 각 끌개의 특성은 다음과 같다.
1) 점끌개의 경우, Under damping된 Forced oscillation으로서 위상공간에서는 한 점으로 수렴한다.
2) 주기성 끌개의 경우, sine 함수를 이용하며, 위상공간에서 닫힌 폐루프를 구성한다.
3) 준주기 끌개의 경우, 무리수비를 이루는 두 개의 주파수를 중첩했으며, 위상공간에서는
torus형의 궤적을 보이며 그 푸앙카레 단면은 폐루프를 구성한다.
4) strange attractor는 위상공간에서 겹치지 않는 무한대의 궤적을 생성할 것이며, Lorenz attractor는 두 개의 회전상을 오가는 형태의 해구조를 형성한다.
본 절에서는 3.1절에서 언급한 시간지연 방법을 이용하여 3차원 위상공간상에 각 형태의 attractor를 재구성하고 푸앙카레 단면을 통해 그 특성을 도시하기로 한다.
시간지연 방법을 사용할 경우, 1)-3)항은 생성 규칙상 2-axis return map으로 끌개를 구성하는 것이 원칙이나, 3차원으로 구성할 경우 동일한 위상 특성을 보이며, 푸앙카레 단면의 설명과 이해의 편의를 위해 3차원 위상 공간을 택하기로 한다.
일반적인 strange attractor 구성의 차원을 선택하기 위해서는 상관 차원등의 factor들이 필요하나 본 고에서는 기본 형태에 대한 1차적인 이해를 목적으로 하므로 2-3차원에서의 구성만은 언급할 것이다.
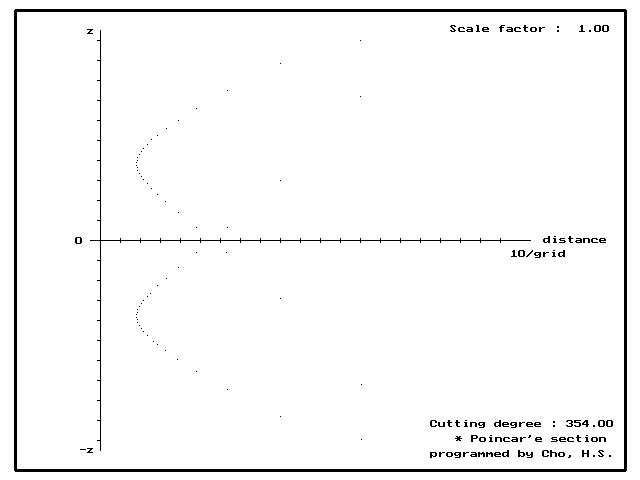
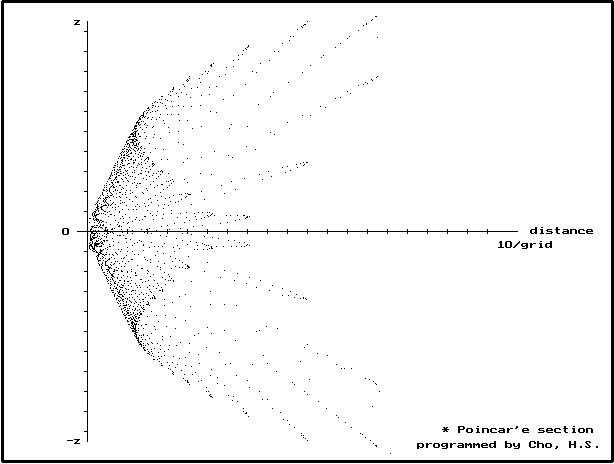
푸앙카레 단면을 구성하기 위하여 본 연구에서 사용한 방법은 xy 평면상에 y=0축을 0으로 하여 360도를 회전하는 임의의 yz평면을 각 각도에 해당하는 푸앙카레 단면으로 정의하였으며,
푸앙카레 단면이 지나가는 xy평면상에 사영된 궤적의 기울기와 함께 yz평면의 기울기를 구하여 xy평면상에서 푸앙카레 단면에 해당되는 선분을 지나가는 상태의 y좌표를 구하여 해당지점까지의 xy평면상의 유클리드 거리를 x축, 해당 지점의 z값을 y축으로 하여 2차원 평면에 도시하는 방법을 취했다. 위의 두 가지 방식은 외부 파일로부터 입력된 임의의 데이터를 동일한 방법으로 처리하여 계의 동역학의 특성을 파악할 수 있게 하였다.
3.2.1. 점끌개 (node, Transient, Forced Oscillation)
(a) 시계열 데이터
(b) 시간 지연 재구성 (3-dimension, delay 15 degree).
Fig. 2. 점끌개의 구조.
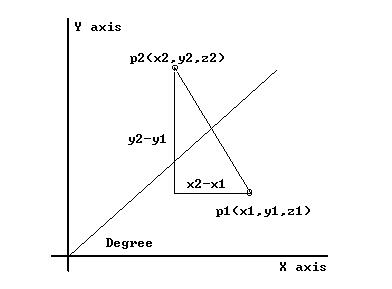
Fig. 3. 푸앙카레 단면의 계산 방법
* 푸앙카레 단면의 교차점 추적용 기울기 산출 (y,z 값)
3.2.2. 주기 운동 (periodic, sine vibration)
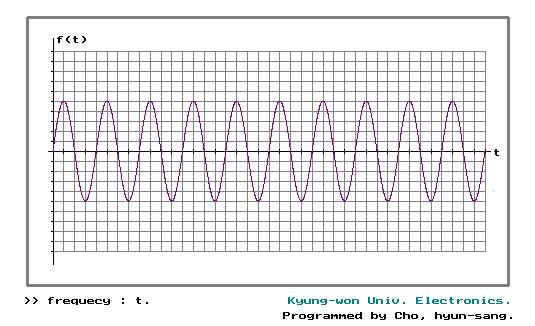
(a) 시계열 데이터.
(b) 시간 지연 재구성.
(c) Poincar 단면 (0-360o, +6o).
Fig. 4. 주기 운동의 구조.
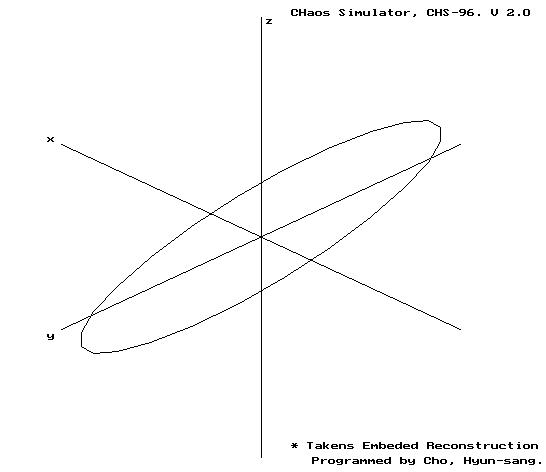
3.2.3. 준주기 운동 (quasiperiodicity, non-rational ratio)
(a) 시계열 데이터.
(b) 시간 지연 재구성.
(c) Poincar 단면 (0-360o+ +6o)
Fig. 5. 준주기 운동의 구조. (y=sin t +sin root 2 t)
3.2.4. 혼돈 현상 (Chaos, Lorenz attractor)
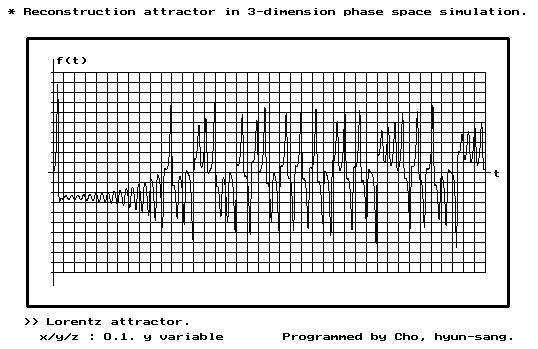
Fig. 6. 혼돈 현상(Lorenz attractor)의 시계열 데이터
3.3. 예측 불가능성 (Butterfly effect)
카오스 현상에 대한 연구 재시작의 중요한 계기가 되었던 로렌츠의 대류방정식에서의 중요한 결론 중 하나는 결정론적인 비선형계의 해 구조가 근본적으로 예측 불가능하다는 것이었다.
그 이유는 비선형 방정식의 해구조가 갖는 잡아당겨지고(stretching) 접혀지는(folding) 경향의 혼합에 기인한다.
따라서 초기값의 조그마한 차이는 계속된 attractor 해 구조로의 사상이 반복 될수록 서로 멀어지게 되며, 종국에는 거의 비슷하게 출발한 두 개의 위상 공간상의 궤적은 서로 완전히 상이한 궤도를 돌게 된다.
중요한 점은 이 두 가지 상이한 궤도는 strange attractor의 해 구조 자체를 벗어나지는 않는다는 점이다.
본 절에서는 Logistic map과 Lorenz attractor의 3차원 display에서의 나비효과를 도시하였다.
3.3.1. Logistic map (time series)
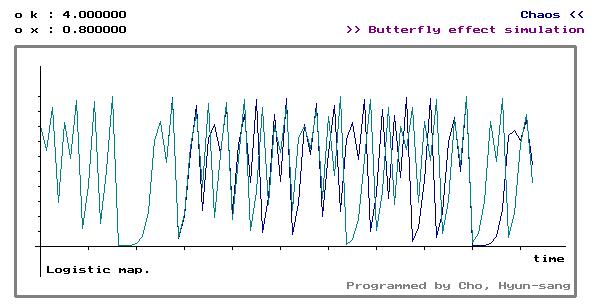
Fig. 7. Logistic map에서의 나비 효과. (시계열 데이터)
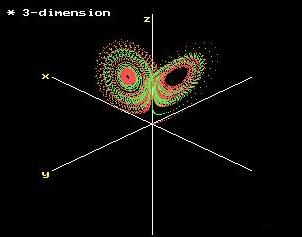
Fig. 8. Lorenz attractor에서의 나비 효과.
녹색과 빨간색의 두가지 초기치에 의한 궤적이 상이함을 그림을 통해 알 수 있다.
이 결과를 통하여 전술한 바와 같이 나비효과를 유발하는 strange attractor의 성질을 확인할 수 있다.
3.4. 갈래질 (Bifurcation)
서론에서 언급한바와 같이 bifurcation diagram은 파이겐바움에 의해 그 축척률의 보편성이 연구된 주제이다.
Bifurcation은 비선형계에서 특정변수의 변화에 따라 나타나는 해의 변화를 도시한 것이다.
본 연구에서는 해당 계에 대해 600번의 반복연산 후 300회 이후의 300개의 값을 취하여 plot하는 방법으로 bifurcation diagram을 구성하였다. 또한 외부 파일로부터 데이터를 입력을 받아서 display하여 계에서 일어나는 bifurcation 현상을 연구할 수 있게 하였다.
3.4.1. Logistic / Trigonometric map
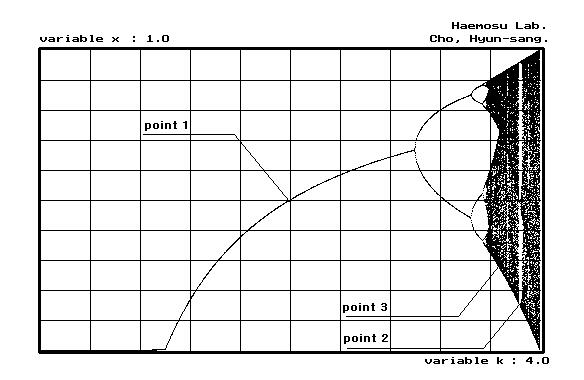
(a) Logistic map.
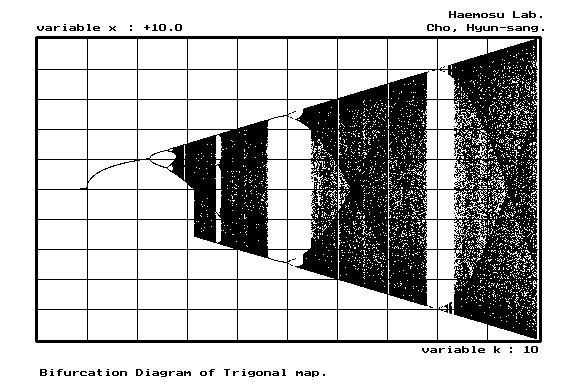
(b) Trigonal map. (초기 값 : 7)
Fig. 9. Logistic / Trigonal map의 bifurcation diagram.
3.4.2. Bifurcation diagram 각 부분에서의 attractor와 시계열 데이터의 상태.
Bifurcation diagram의 특징중의 하나는 diagram으로부터 attractor의 형태를 유추할 수 있다는 점이다.
본 절에서는 요크의 논문에 언급된 주기 3영역의 주기성 창문(periodic window)의 특성을 포함하여 전 절에서 다룬 bifurcation diagram의 특정 지점에 대한 시계열 데이터와 attractor의 형태를 고찰하므로써 혼돈현상의 특징을 종합적으로 검토한다.
특히 주의할 사항은 fig 9의 point 2 지점에 대한 시계열 데이터로서 전반부의 복잡한 양상이 0.152074/0.494514/0.958635 의 3주기 영역으로 수렴하는 모습이다.
시뮬레이션의 결과 초기값의 설정에 따라 나비효과를 위해 비교되는 미소하게 차이가 나는 두 개의 궤적은 동일한 주기에 조금 다른 시차를 두고 진행하는 경우도 발견되었다.
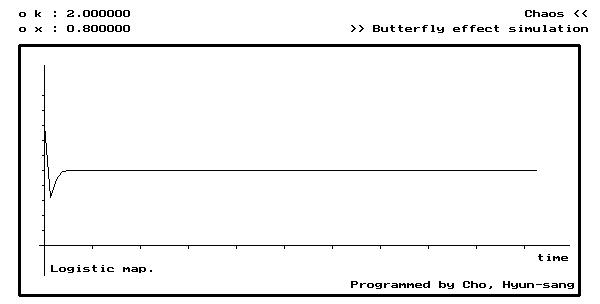
(a) 시계열 데이터.
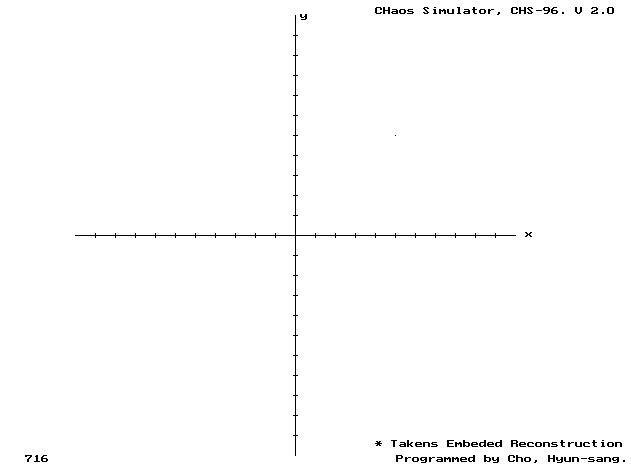
(b) 재구성.
Fig. 10. Point 1. 에서의 시계열 데이터와 attractor (정상상태 수렴, k=2.0)
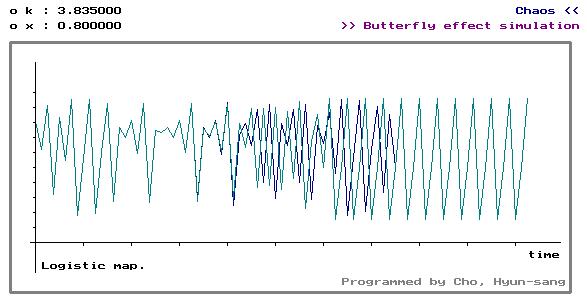
(a) 시계열 데이터.
(b) 재구성. (phase locking)
Fig. 11. Point 2. 에서의 시계열 데이터와 attractor (주기 3, periodic window, k=3.835)
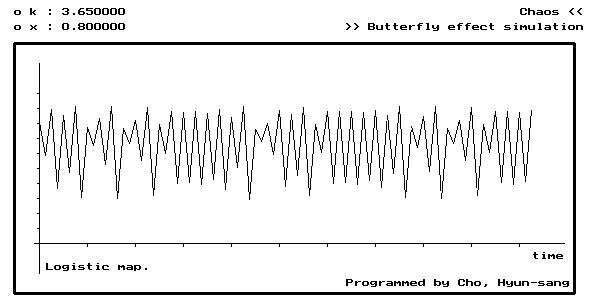
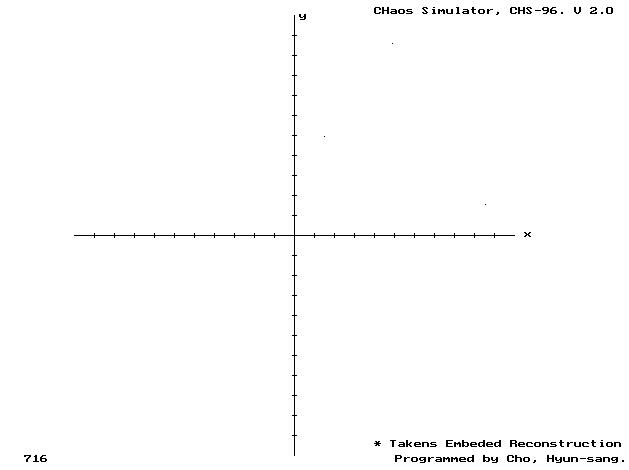
(a) 시계열 데이터.
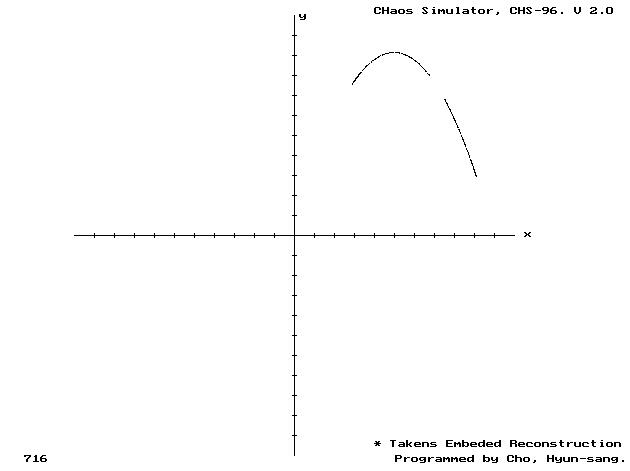
(b) 재구성.
Fig. 12. Point 3. 에서의 시계열 데이터와 attractor (Chaos, k=3.65)
IV. 카오스 시뮬레이터 CHS(CHaos Simulator)-96.
4.1. 개요.
카오스 시뮬레이터 CHS-96은 지금까지 고찰한 혼돈현상의 일반적인 특성을 그래픽으로 도시할 수 있도록 구성되어 있다.
또한, 사용자는 외부에서 입력된 데이터에 대해 타켄스 매립정리를 통한 attractor의 파악과 구성된 attractor에 대한 푸앙카레 단면을 조사할 수 있으며, 외부의 bifurcation 자료에 대한 입력에 대해 동일한 분석을 할 수 있다.
이러한 기능을 확장하면 푸앙카레 단면을 통해 카오스성의 주요 판단 요소인 리아푸노프 지수와 상관차원을 산출할 수 있으며 바이퍼케이션을 통해 마찬가지로 계의 동역학적인 특성을 추정할 수 있다.
전체 시뮬레이터는 프로그램 패키지의 형식으로 나비효과 시뮬레이터 2개와 attractor 시뮬레이터 1개의 외부 실행 file로 구성되어 있다.
주 시뮬레이터는 세 개의 source file이 project file로 구성되어 TC 2.0으로 컴파일 되었다.
첫 번째 file은 3차원 display와 푸앙카레 단면 기능을 포함하는 모듈이 구성되어 있으며 두 번째 file은 그래픽 메뉴와 택스트 메뉴로 구성되었고 마지막 세 번째 file은 bifurcation에 관련된 모듈로 구성되어 있다.
외부 data file은 일반 택스트 에디터로 작성할 수 있으며 최대 10800개의 float형 변수가 입력 가능하다.
TET에 해당되는 data file은 확장자 '*.CHS'로 저장되어야 하며, bifurcation 에 해당하는 data file은 확장자 '*.BIF'로 저장되어야 한다.
data file들은 현 작업 디렉토리에 있어야 하며, 최대 12개까지 menu-bar형식의 그래픽 메뉴에 등록된다.
메뉴간 이동은 커서와 CR, ESC를 이용하며, 텍스트 메뉴에서는 메뉴선택이 끝났을 경우 'q'를 이용하여 메뉴 항목선택을 종료한다.
4.2. Menu 구조.
1] Main menu
1) Mathematical model. →수식으로 기술되는 attractor 모델군
2) Outer Data (TET) →외부 데이터에 대한 TET 조건 선택.
3) Butterfly effect, Logistic.
4) Butterfly effect, Trigonal.
5) Bifurcation, Logistic.
6) Bifurcation, Trigonal.
7) Outer Bifurcation.
8) Attractor.
9) Quit.
1-1] Mathematical model.
1) Sine vibration. →주기 운동에 관한 attractor.
2) Transient state. →점끌개
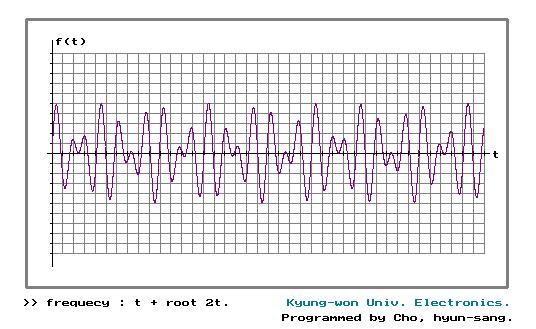
3) Aperiodic (t+2t). →유리수비 진동수 중첩.
4) Aperiodic (t+root(2)). →무리수비 진동수 중첩.
5) Aperiodic (t+pi(t)).
6) 3 period s.p. vibration. → 무리수비 3주기 중첩.
7) Logistic map (standard).
8) Logistic map (under, 2t). →logistic map under sampling.
9) Trigonal map.
10) Random. → Stochastic process.
11) Lorenz attractor. →x variable.
12) R ssler attractor. →y variable.
1-2] Outer TET processing. (default : sine vibration)
1) Zoom rate (2-dimension). →Scale.
2) Zoom rate (3-dimension).
3) Zoom rate (Poincar section).
4) Start (2-Dim). →시계열 데이터 display를 위한 data 시작 주소.
5) End (2-Dim). →끝 주소.
6) Start (3-Dim). →3차원 재구성을 위한 data 시작주소.
7) End (3-Dim).
8) Sampling period (3-Dim).
9) Start of P-section (d). →푸앙카레 단면의 시작 각도.
10) End of P-section (d). →종료 각도.
11) Increase deg of P-sec. → 각도 증분.
12) End of data for P-sec. →푸앙카레 단면 구성에 사용될 data 끝주소.
13) Display (1:dot,2:line). →시계열 데이터 display 상태.
14) Display speed. → 확대 위상공간 display 속도.
15) Display select (2/3). →위상공간상의 attractor의 구성 차원.
16) 2-Dimension scale. →2차원 return map 구성시의 scale.
1-3/4] Butterfly effect simulation. (외부 file)
1) Input k (0-4). →선도변수(번식률).
2) Input x (0-1). →초기값.
3) Signal Modify ? (y/n, 'q' for quit).
1-5/6] Bifurcation simulation. (Logistic/Trigonal)
1) Default mode. →0-4 (log) / 0-10 (Tri)
2) Setting value (interval).
2-1) Start point (0-4.0).
2-2) Ending point (0-4.0).
2-3) Increasement (<4.0).
2-4) Initial value (<1.0).
3) Quit selection.
1-7] Outer Bifurcation simulation.
1) Starting step.
2) Ending step.
3) Scan size. →한 변수 step에 display되는 변수의 갯수.
4) Zoom rate. →Scale.
1-8] Attractor simulation.
1) Lorenz attractor.
2) Lorenz, Butterfly effect.
3) R ssler attractor.
4) R ssler, Butterfly effect.
5) Quit.
V. 결 론.
지금까지 혼돈현상에 대한 연구의 간단한 역사와 일반적인 특성, 학습과 연구를 위한 시뮬레이터 개발의 필요성과 함께 전술한 목적을 위해 개발된 시뮬레이터 CHS-96과 그 결과의 타당성에 대해 서술하였다.
도시된 시뮬레이션의 결과는 이론에서 예측하는 바와 부합하고 있다. 혼돈현상은 그 반복계산량의 방대함으로 인해 고성능 계산기가 발전된 근래에 이르러서야 발전하기 시작한 학문이다.
따라서 혼돈현상을 연구하기 위한 시뮬레이터의 개발은 전산기를 이용한 혼돈 현상에 대한 연구 자체에서도 그 의미를 찾을 수 있을 것이다.
차후의 연구를 통해 개선되어야 할 주요 문제점으로는
첫째, 푸앙카레 단면의 구성시의 오차를 들 수 있다.
이 부분은 변수의 형태를 double형으로 바꾸어 유효 자리 수를 늘리며, 현재 xy평면의 기울기의 분모 부분을 구성하는 Δ가 0로 접근할 때 단순히 그 결과를 회피하도록 되어 있는 기울기 처리 부분을 수정하므로써 개선될 수 있을 것이다.
또한, 정밀도가 어느 정도 이상 확보된 후에 수작업으로 계산해야 하는 리아푸노프지수와 상관차원의 자동계산이 가능할 것이다.
둘째로, 시계열 데이터의 주파수 대역에 대한 FFT (Fast Fourier Transform) 분석 기능이 추가되어야 한다.
혼돈현상으로 이르는 bifurcation diagram에 나타나 있는 주기배증은 주파수 영역의 power spectrum을 통해 보다 상세한 관찰이 가능하다.
혼돈영역에 있어서의 power spectrum은 거듭된 주기배증의 결과 주파수 band의 형태를 가지게 된다.
연구과정에 시뮬레이터 외적으로 Goertzel 알고리즘을 이용한 DFT (Discrete Fourier Transform)을 통해 이러한 사실을 확인할 수 있었으나 아직은 프로그램 내부에는 포함된 기능이 아니기 때문에 본 고에서는 기술하지 않았다.
혼돈현상에 대한 연구는 학문의 어느 한 분야에만 치중되어 있지 않으며 마치 뉴튼 패러다임이 사회 각분야에 미친 영향과 같이 여러 분야에서 공통적으로 발견되어 연구되고 있다.
서론에서 언급한 바와 같이 현재는 산타페 연구소를 중심으로 기존의 동역학계의 구분, 즉 질서와 혼돈의 사이에 존재하는 '복잡성'이라는 현상으로 연구의 진전이 되고 있으며 우리 자신을 포함하는 생명의 현상의 본질도
혼돈의 가장자리 (Edge of Chaos, Christopher G. Langton)에서의 자기 조직화와 적응 진화 현상으로 파악되고 있는 것이다.
그러나, 이러한 형태의 진전된 연구에는 마치 선형 해석학을 이해하지 못하는 사람의 비선형 둥역학에 대한 접근이 곤란하듯 혼돈 현상에 대한 이해가 없다면 어느 한계 이상의 접근은 곤란하다고 할 수 있다.
본 연구의 내용과 결과는 차후 혼돈현상에 대한 개론적인 이해와 정성적인 파악을 필요로 하는 경우에 그 이해를 도울 수 있을 것이며,
더 나아가 혼돈을 근간으로 인문 / 사회과학을 포함하는 새로운 연구와 혼돈 현상을 통한 보다 발전된 시각의 확보에 기여할 수 있을 것으로 기대된다.
참고 자료.
1. Ian Stewart, 박 배식/조 혁, "Does God Play Dice ?, The Mathematics of Chaos.", 범양사 출판부. 1993.
2. James Gleick, 박 배식/성 하운, "Chaos, Making a New Science", 동문사. 1993.
3. 合原一辛, 과학세대, "Chaos", 한뜻. 1994.
4. 合原一辛외 5인, 정 호선/여 진경, "뉴로.퍼지.카오스, 신세대 아날로그 컴퓨팅 입문", 대광서림. 1994.
5. 合原一辛 편저, 정 호선/여 진경, "뇌와 카오스", Ohm 사, 1994.
6. Erwin Kreyszig, "Advanced Engineering Mathematics 7th Edition", John Weiley & Sons, Inc. 1993.
7. Brain Lab, "뇌전위와 카오스", 한국과학기술원 물리학과 센서공학연구실, Sep. 1. 1995.
8. 안 현순, "터보 C로 구현한 과학기술 계산 프로그래밍", 가남사. 1995.
9. M. Mitchell Waldrop, 김 기식/박 형규, "Complexity", 범양사출판부. 1996.
10. 조 현상, "A Study on a Evolutionary Processes of Neural Network in a Pattern Recognition Problems", 경원대학교 전자공학과 제11회 학술 발표회. 1996.9.
* V 2.2 추가 기능.
main menu 9 : random함수와 logistic 함수의 0-1간의 난수 분포 상태 display.
logistic의 경우, 메뉴 선택시 k 변수의 입력을 요구한다. k값의 변화에 따라
난수의 분포는 차이를 보일 것이다.
발생하는 난수의 분포도는 y축의 최대값에 비례하여 정규화되며 정규화되어
조정된 factor는 y축의 상단에 표시된다. 현재의 실제 분포상태는 거의 uniform한
random 함수의 분포 상태와 비교하여 판단할 수 있다.
Chaos simulator, CHS-96 (Program Download)